This paper demonstrates that the 3D depth perceived by a viewer on a 3D image is a function of the viewing distance. The larger the viewing distance, the deeper the depth. Through some geometrical relationship, we can conclude that objects that are behind the lenticular sheet are more sensitive to objects that are in front to the changing viewing distance.
3D lenticular printing is based on the principle of binocular disparity. Human sees the world in 3D because of the fact that our left eye and our right eye see with slightly different images. Our brains combine these two images to create the sense of depth.
3D Lenticular printing is an artificial way to create such binocular disparity. The diagram below illustrates the principle.
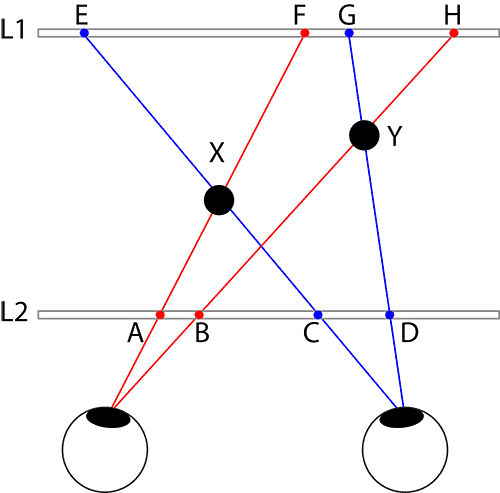
Figure 1. Principle of 3-D explained by binocular disparity
For spatial objects X and Y, the left eye sees them from the rays LX and LY. Similarly, the right eye sees them as RX and RY. The viewing angles differ for the same objects when viewed by the left eye and the right eye. It is this difference in "perspective" that creates the necessary binocular disparity for 3D perception.
Let us refer to the diagram again. If a 3-D print L2 is made such that the image of X is put at position A and C, and the image of Y is put at position B and D, then through the selective light re-direction of the lenticular sheet, both eyes will be fooled into thinking that Object X and Object Y are at the spatial positions behind the sheet. Similarly, for 3D print L1, if the image of X is put at position E and F, and the image of Y is put at position H and G, then the eyes will be deceived as if objects X and Y are in front of the plastic sheet.
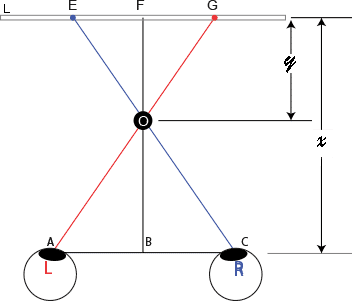
Figure 2 Relationship between viewing distance and depth - Object in from of lenticular sheet
In Figure 2, E is the image of O intended for the right eye, and G is the image of O intended for the left eye. Based on the explanation in the last section, we know that this will create an illusion that Object O is popping out of the plastic sheet at a distance y. With simple geometrical knowledge that triangle OEG and OAC are similar triangles, we can express y as a function of x (the viewing distance) as follows.
$$ \frac{y}{EG} = \frac{x-y}{AC} --------- (1)$$
or$$ y = \frac{EG}{(AC + EG)}x ------- (2)$$
Clearly, the depth y is proportional to viewing distance x as both EG and AC are constants.
The rate of change of depth vs the changing viewing distance can be expressed as
$$ \frac{dy}{dx} = \frac{EG}{AC + EG} = C1----- (3)$$
In the case when the object is behind the sheet, we can use the same geometrical properties to come up with another relationship.
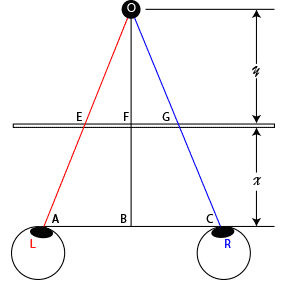
Figure 3. Relationship between viewing distance and depth - Object behind of lenticular sheet
In Figure 3, we can see that
$$ \frac{y}{EG} = \frac{(x + y)}{AC} -------- (4)$$
or$$ y = \frac{EG}{(AC - EG)}x------- (5)$$
Again, the depth y is proportional to the viewing distance x. The rate of change in depth against the change of viewing distance is
$$ \frac{dy}{dx} = \frac{EG}{AC-EG} = C2 ----- (6) $$
Recap that we had
$$ y = \frac{EG}{(AC + EG)}x $$ for objects that are perceived to be in front of the pirnt, and
$$ y = \frac{EG}{(AC - EG)}x $$ for objects that are perceived to be behind the print.
From these, we can conclude that the perceived depth is always proportional to the viewing distance. When the viewing distance is short, the perceived 3D depth is relatively shallow. When the viewing distance is long, the perceived 3D depth is relatively deep.
By taking the derivative of the perceived depth to the viewing distance, we came up with the rate of change of depth vs the change of viewing distance, and they are
$$\frac{dy}{dx} = \frac{EG}{AC + EG} = C1 $$ and
$$\frac{dy}{dx} = \frac{EG}{AC - EG} = C2 $$
It is obvious that C1 < C2, and from this fact, we can also conclude that the perceived depth for objects behind the lenticular sheet is more sensitive to that of the ones in front. In other words, when one moves away from a lenticular print, i.e,. increasing the viewing distance, the speed of objects receding from the picture is faster than the objects moving towards the viewer.